Tilbake til lesekroken
STATOSKOPET
(Erik Nord, 1999)
En hjelp til å forstå elementær statistikk og til å
bedømme usikkerhet i forskningsresultater basert på tilfeldige utvalg. Følgende begreper forklares: 1 Variasjon
og normalfordeling 2
Standardavvik 3
Utvalgsvariasjon og standardfeil 4
Konfidensintervall 5
Standardfeilen for en prosentandel 6
Standardfeilen for en forskjell 7 P-verdi 8 T-verdi 9
Korrelasjonsanalyse 10 Regresjonsanalyse 11 Forklart varians 12 Relativ risiko 13 Oddsratio 1 Variasjon og normalfordeling: Enhver egenskap eller effekt av et tiltak i en
populasjon har en spredning rundt et gjennomsnitt. En normalfordeling er en
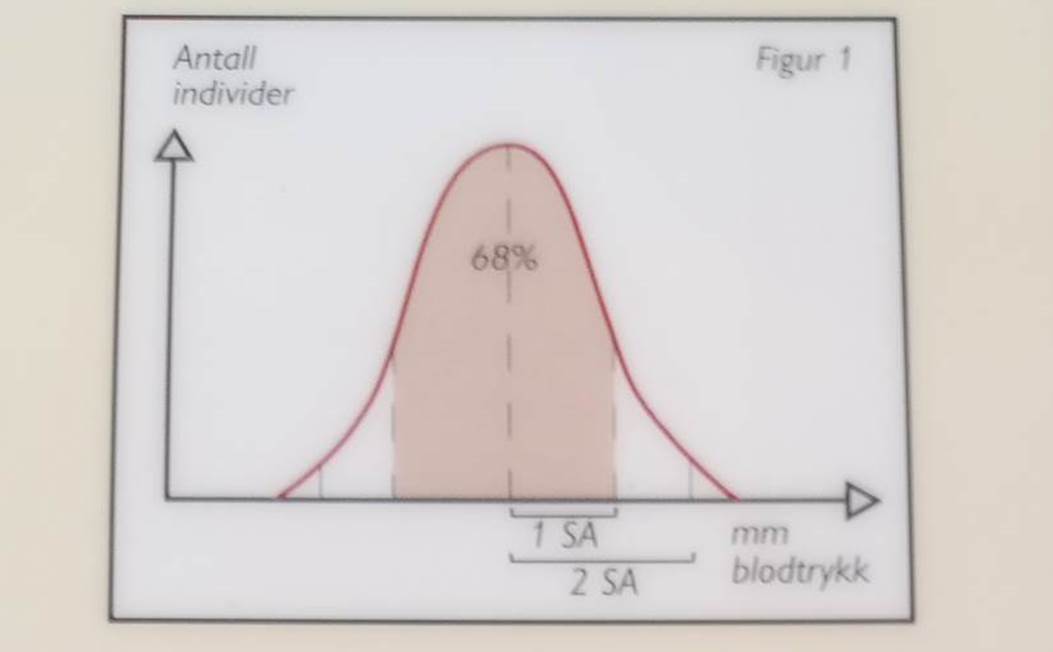
symmetrisk, klokkeformet spredning om midtpunktet, se figur 1.
2 Standardavvik (SA) er
et mål på graden av spredning rundt gjennom-snittet. I en normalfordeling
angir et standardavvik den avstand fra gjennomsnittet som 68 prosent av
populasjonen ligger innenfor. 95
prosent av en normalfordelt populasjon ligger innenfor en avstand av 2
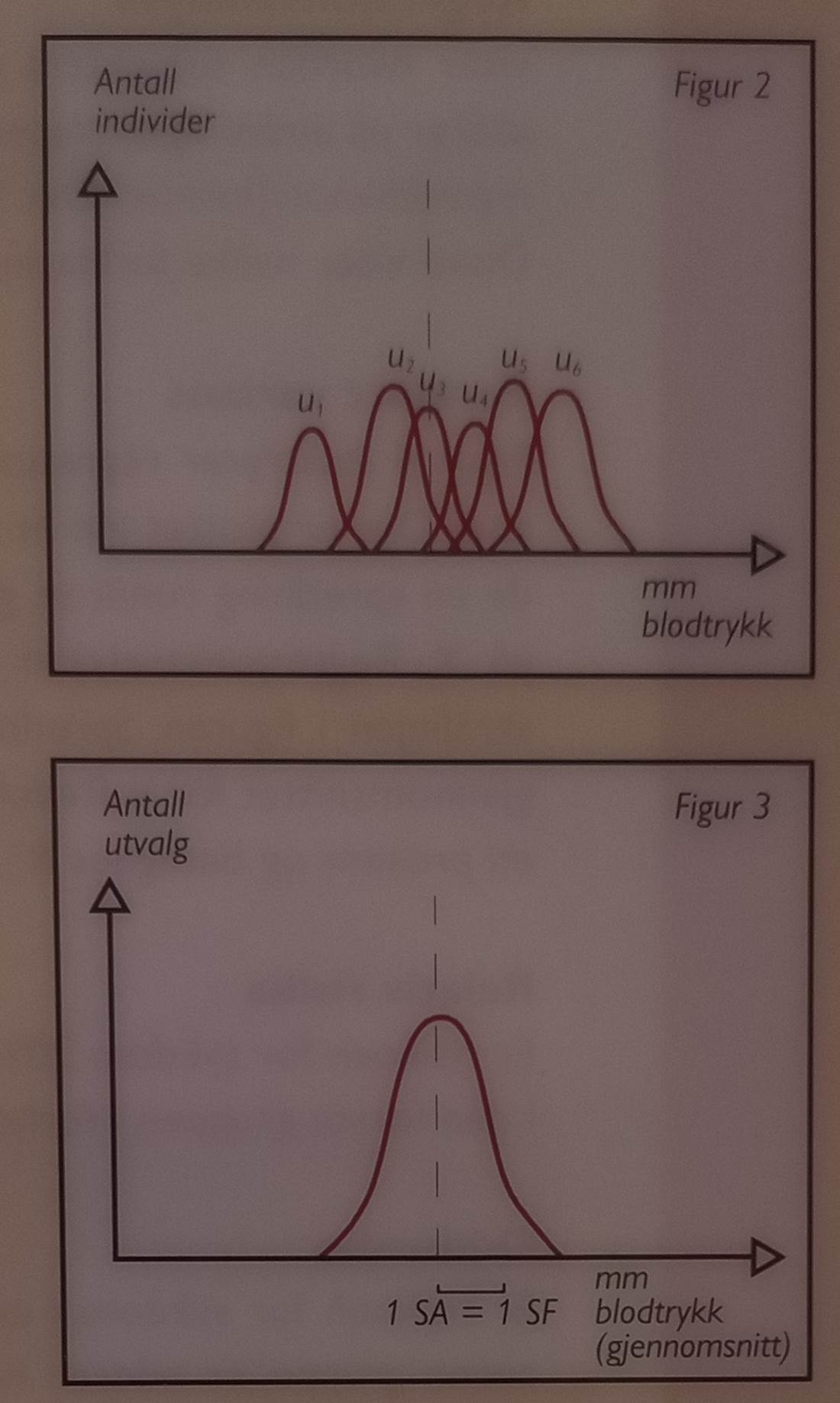
standardavvik fra gjennomsnittet (figur 1). 3 Utvalgsvariasjon og standardfeil: Trekker man flere tilfeldige utvalg fra samme
populasjon, vil gjennomsnittsverdiene i utvalgene variere noe rundt
gjennomsnittsverdien for populasjonen som helhet (figur 2).
Graden
av spredning i gjennomsnittene kan uttrykkes ved deres standardavvik. Dette
standardavviket forteller hvor stor unøyaktighet man må forvente hvis man
generaliserer til populasjonen som helhet ut fra gjennomsnittet i et enkelt
utvalg. Gjennomsnittenes standardavvik kan anslås ved at man dividerer
standardavviket i det utvalget man har trukket med kvadratroten av antall
personer (N) i utvalget (eksempel 1). Resultatet kalles standardfeilen (SF) for gjennomsnittet i utvalget når
dette brukes som estimat for gjennomsnittet i populasjonen. Se figur 3. Eksempel 1: I et utvalg på 100 er
gj.snittsblodtrykket 130 mm og standardavviket 20 mm. => SF = 20/100 = 2
mm. 4 Konfidensintervall: Gjennomsnittet i populasjonen som helhet ligger
med 95 % sannsynlighet innenfor en
avstand av 2 standardfeil fra
gjennomsnittet i utvalget. Området ’utvalgsgjennomsnitt +/- 2 standardfeil’
kalles 95-prosent
konfidens-intervallet (KI) for
gjennomsnittet i populasjonen (eksempel 2).
Eksempel 2: I eksempel 1
er 95 % KI = 130 +/- 2x2 =126–134 mm. 5 Standardfeilen for en prosentandel: Ofte måles
prosentandelen (P) som har en bestemt egenskap, snarere enn
gjennomsnittsskåren på egenskapen. SF(P) =
P(100-P)/N, når N er
utvalgsstørrelsen (eksempel 3). Note 3: 100 fikk medisin, 10 % ble friske. => SF(P) = (10x90)/100
= 3 %. 6 Standardfeilen for en forskjell mellom to gjennomsnitt eller to
prosentandeler: SF(Diff) = SF12
+ SF2 2
, der SF1 og SF2 er standardfeilene for hvert av gjennomsnittene/prosentandelene
(eksempel 4). Eksempel 4: 60 % av 100
reagerte positivt på medikament
A, mens 50 % i en annen tilfeldig
gruppe på 144 personer reagerte
positivt på placebo. => SF1
= 4.9 %, SF2 = 4.2 %, SF(Diff) = 6.4 %,
KI = 10 +/- 12.8 %, dvs fra –2.8 %
til +22.8 %.
7 P-verdi: På
grunn av tilfeldig variasjon kan grupper som egentlig er like, skåre ulikt i
utvalgsundersøkelser. Anta at en undersøkelse viser en viss forskjell mellom
to grupper. Sannsynligheten for å
trekke et utvalg som viser minst så stor forskjell når det egentlig ikke er
forskjell, kalles forskjellens p-verdi
(eksempel 5). Jo lavere p-verdien er, jo mer statistisk signifikant anses den observerte forskjellen å være.
Eksempel 5. Forekomsten av
en sykdom var 10 prosent i en behandlingsgruppe på 100 personer, mot 15
prosent i en like stor kontrollgruppe. Sjansen for å finne en så stor
forskjell hvis behandlingen i virkeligheten var virkningsløs, er 28 %. Dvs. at den observerte forskjellen har
en p-verdi på 0.28. NB! Den vekten en bør
tillegge en observert forskjell avhenger på den ene side av p-verdien, og på
den annen side av hvor rimelig forskjellen virker ut fra det en ellers vet.
Er forskjellen uforståelig, vil en betrakte den som tilfeldig med mindre
p-verdien er svært lav. 8 T-verdi: Dividerer man
en forskjell på forskjellens standardfeil (se foran), får man forskjellens
t-verdi, se eksempel 6. Høy t-verdi betyr at forskjellen er stor i forhold
til den statistiske feilmarginen, og derfor overbevisende. Det er en direkte
sammenheng mellom t-verdier og p-verdier. Har man mange observasjoner,
gjelder tallene til høyre.
Eksempel 6. Observert en forskjell på 20 mm blodtrykk mellom en behandlingsgruppe
og en kontrollgruppe. SF beregnes til
å være 10 mm. => t-verdi = 2.0. t-verdi: 1.0
1.5 1.7 2.0
2.6 p-verdi: 0.32 0.13
0.09 0.05 0.01 9 Korrelasjonsanalyse forteller hvor sterkt to egenskaper samvarier i et utvalg av subjekter. Samvariasjonen uttrykkes som en
koeffisient r mellom –1 og +1.
Standardfeilen for r brukt som estimat for hele populasjonen: SF(r) = (1 – r2) / N, når N er utvalgsstørrelsen (eks. 7). Note 7.: N = 100, r = 0.8
gir SF (r) = 0.036 og 95% KI = 0.8 +/- 0.072 = 0.73 – 0.87. 10 Regresjonsanalyse viser hvordan
subjekters skåre på én egenskap (avhengig variabel) påvirkes av deres skårer
på andre egenskaper (forklaringsvariable), se eksempel 8 på såkalte ustandardiserte
regresjonskoeffisienter. Det kan også beregnes standardiserte koeffisienter, se eksempel 9. Disse viser hvilke forklaringsvariable som betyr mest for den
avhengige variabelen. Eksempel 8. Ustandardisert
regresjons-likning. Blodtrykk = B + 0.8 x
År + 0.6 x Kg. Likningen forteller at blodtrykket i gjennomsnitt øker med 0.8 mm per år ved uendret kroppsvekt, og
med 0.6 mm når kroppsvekten øker med en kilo og alderen er uendret. Eksempel 9.
Anta at man sammenlikner personer med gjennomsnittlig kroppsvekt med
personer med kroppsvekt et standardavvik over gjennomsnittet. Personene er
ellers like. Anta at blodtrykket hos de sistnevnte ligger et halvt
standardavvik over gjennomsnittlig blodtrykk. => standardisert
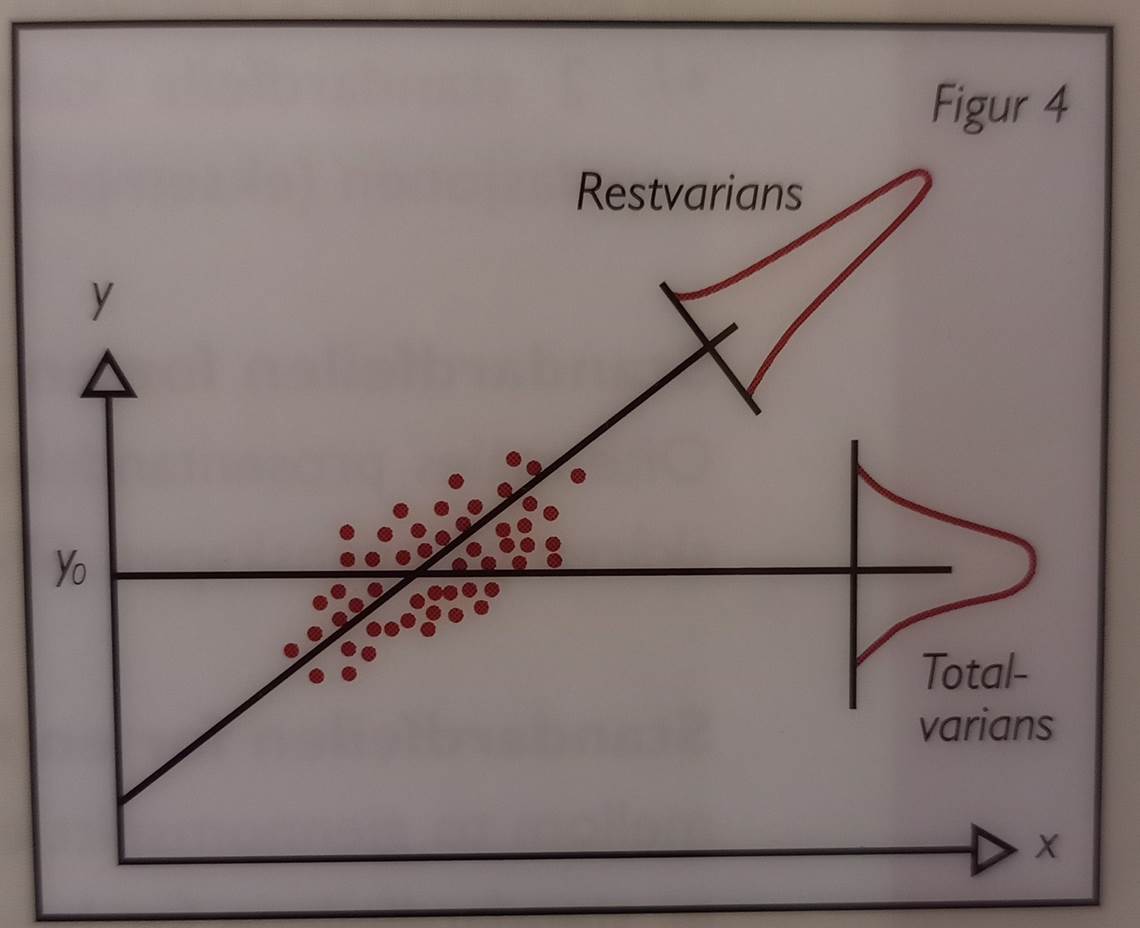
regresjonskoeffisient = 0.5. 11 Forklart varians: Figur 4 illustrerer regresjonsanalyse i det enkleste
tilfellet med bare en forklaringsvariabel. Det er plottet inn et utvalg
personer med skårer på egenskapene X og Y. På Y har de en spredning rundt et
gjennomsnitt y0. Noe av
denne spredningen skyldes spredning på X. Regresjonsanalysen anslår gjennomsnittsverdier for Y gitt ulike verdier for X, jfr
skrålinjen i figuren. Spredningen
rundt denne linjen er mindre enn spredningen
rundt gjennomsnittet for y.
Reduksjonen i spredning kalles forklart
varians. Den beregnes som en prosent og betegnes R2. Høy R2
indikerer at forklaringsmodellen som helhet er god.
12 Relativ risiko: Er risikoen for sykdom 20 % i
en gruppe og 10 % i en annen, er den relative risikoen (RR) i den første
gruppen 20:10 = 2.0. 13 Oddsratio: Er risikoen for sykdom i en gruppe 20 %, er
oddsen 20/80 = 1/4. Er risikoen 10 % i en annen gruppe, er oddsen her 10/90 =
1/9. Oddsratioen (OR) blir da: ¼ : 1/9
= 2,25. Oddsratio er tilnærmet lik
relativ risiko hvis begge risikoer er under 20-30 %, se tabellen.
|